[BoostCamp]Day1 기초 수학
부스트캠프 1일차 공부 정리.
1일차 공부 정리
무어-펜로즈(Moore-Penrose) 역행렬
우선 역행렬부터 간단히 정의하면 어떤 행렬에 대해 행렬곱을 진행할 때(방향 상관 없이) 항등행렬이 나오는 행렬을 그 행렬의 역행렬이라고 합니다.
행과 열 길이가 같고 행렬식이 0이 아닌 경우 역행렬은 항상존재합니다만, 앞으로 다룰 행렬이 대부분 행과 열 길이가 다른 행렬입니다.
이 경우 행렬 곱 순서에 따라 다른 행렬이 나오기 때문에 역행렬을 정의할 수 없습니다.
다만 역행렬에 기능을 유사하게 수행하기 위해 무어-펜로즈 역행렬을 다음과 같이 정의합니다.
행이 열보다 길이가 긴 경우 $A^+ = (A^TA)^{-1}A^T$, 열이 행보다 길이가 긴 경우 $A^+ = A^T(A^TA)^{-1}$ 입니다.
행이 열보다 길이가 긴 경우 $A^+A = I_{m}$, 열이 행보다 길이가 긴 경우 $AA^+ = I_{n}$ 을 만족합니다.
행과 열 중 길이가 작은 값 기준으로 항등행렬이 생성된다고 생각하면 기억이 오래갈 것 같네요.
몬테카를로 샘플링
기계학습을 진행하게 되면 확률분포를 명시적으로 모르는 경우가 대부분입니다.
확률분포를 모를 때 데이터를 이용해서 기대값을 계산하는 방법으로 몬테카를로 샘플링 방법을 사용합니다.
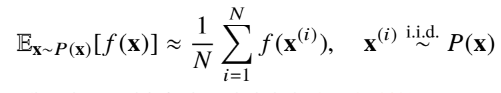
위 수식에서 x는 데이터를, f는 타겟으로 하는 함수를 의미합니다. 데이터들을 추출해 함수에 대입한 뒤 값을 평균내는 식으로 진행하게 됩니다.

예시를 통해 이해하면 쉬운데요. 윗 함수의 [-1,1] 범위 내 적분값을 구하는 것을 몬테카를로 샘플링을 이용해보겠습니다.
import numpy as np
# 범위 내 함수 적분 값 구하는 몬테카를로 샘플링 함수(시뮬레이션)
def mc_int(fun, low, high, sample_size = 100, repeat = 10):
int_len = np.abs(high - low) # x축 길이(범위)
stat = []
# 이 행위 repeat만큼 반복
for _ in range(repeat):
# 범위 내 값 sample_size 만큼 뽑기.
x = np.random.uniform(low = low, high = high, size = sample_size)
# y 값 추출
fun_x = fun(x)
# x축길이(가로) + 평균 구하기(세로)
int_val = int_len * np.mean(fun_x)
stat.append(int_val)
# 평균 뿐만 아니라 반복 수행했기 때문에 표준편차도 구할 수 있음.
# 표준편차로 이 값의 오차범위를 알 수 있음.
return np.mean(stat), np.std(stat)
def f_x(x):
return np.exp(-x**2)
print(mc_int(f_x, low = -1, high = 1, sample_size=10000, repeat=100))
# (1.4941721073750045, 0.0043400930289970545)
# 다른방법으로 계산한 값 : 1.49364
최대가능도 추정법
우선 가능도 함수부터 정의하겠습니다. 가능도 함수란 확률밀도함수와 수식은 같으나 중점으로 보는 변수가 x가 아닌 구하고자 하는 모수 $\theta$입니다.
최대가능도 추정법은 확률밀도함수를 기반으로 한 가능도 함수를 통해서 가장 가능성이 높은 모수를 추정하는 방법입니다.
다만 데이터 집합 x가 독립적으로 추출되었을 경우 가능도 함수가 개별 가능도 함수의 곱으로 표현되어있기 때문에 로그가능도를 사용합니다.
데이터의 숫자가 수억 단위가 된다면 컴퓨터의 정확도로 가능도를 계산하는 것이 힘듭니다.
또 경사하강법으로 가능도를 최적화한다면 미분연산을 사용하는데 로그 가능도함수에 경우 시간복잡도가 $O(N^2)$에서 $O(N)$으로 줄여주는 역할을 합니다.
쿨백-라이블러 발산
기계학습에서 사용되는 손실함수들은 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도합니다.
두 확률분포의 거리는 여러가지 측정 방법이 있는데, 쿨백-라이블러 발산을 소개합니다.
쿨백-라이블러 발산을 최소화하면 분류문제에서 최대가능도 추정법을 이용하는 것과 마찬가지인데요.
정답레이블을 P, 모델 예측을 Q라 두면 쿨백-라이블러 발산의 정의는
$KL(P\parallel Q) = \int_XP(\bold x)log(\frac{P(\bold x)}{Q(\bold x)})d\bold x$ 입니다.
또 $KL(P\parallel Q) = -E_{\bold x \sim P(\bold x)}[log Q(\bold x)] + E_{\bold x \sim P(\bold x)}[log P(\bold x)]$
로 분해할 수 있으며 왼쪽식은 크로스 엔트로피, 오른쪽 식은 엔트로피로 해석할 수 있습니다.
이렇게 분해되는 이유는 통계에서 기대값 정의 $\int_xf(x)P(x)dx = E_{\bold x \sim P(\bold x)}[f(x)]$ 를 응용한 것으로 이해하면 됩니다.
느낀점
첫 시작이라 많이 설레기도 하고 기대되기도 하고 긴장되기도 했습니다.
운영진분들이 좋은 학습여건을 위해 많은 노력을 하고 있다는 것이 느껴집니다.
5개월이 짧은 시간이 아닌 만큼 오버페이스 하지 않고 꾸준히 잘 해보겠습니다.